į┌ųą┐╝öĄ(sh©┤)īWųą╚²ĮŪą╬Ą─┐╝³cę╗░ŃĢ■╔µ╝░ĄĮęįŽ┬ā╚╚▌Ż║
1�Īó╚²ĮŪą╬Ą─ĘųŅÉ����Īó▀ģĮŪĻPŽĄ╝░ąį┘|ĪŻ
2����Īó╚²ĮŪą╬ųąÄūŚlųžę¬Ą─ŠĆČ╬╝░Ųõąį┘|�ĪŻ(ĮŪŲĮĘųŠĆĪóųąŠĆ�ĪóĖ▀ŠĆĪó┤╣ų▒ŲĮĘųŠĆ��Īóųą╬╗ŠĆ)
3��Īó╚½Ą╚╚²ĮŪą╬Ą─┼ąČ©║═ąį┘|����ĪŻ╚½Ą╚╚²ĮŪą╬Ą─┼ąČ©║═ąį┘|╩Ū╚²ĮŪą╬▓┐ĘųĄ─ųž³cā╚╚▌����Ż¼ę╗░Ń╚²ĮŪą╬│Żė├Ą─ėą╦─ĘN┼ąČ©Č©└ĒŻ¼ų▒ĮŪ╚²ĮŪą╬▀ĆąĶ╝ė╔ŽHLČ©└Ē����ĪŻ│²┴╦ąĶ꬚Ų╬š╗∙▒ŠĄ─ąį┘|Īó┼ąČ©�ĪóČ©└Ēų«═ŌŻ¼╚½Ą╚╚²ĮŪą╬│Żė├─Żą═ę▓▒žĒÜę¬╩ņŽż��Ż¼Ž±╩ų└Ł╩ų─Żą═║═ę╗ŠĆ╚²Ą╚ĮŪ─Żą═Ż¼į┌┐╝įćųą│÷¼F(xi©żn)Ą─Ņl┬╩▒╚▌^Ė▀�ĪŻ

4ĪóĄ╚č³╚²ĮŪą╬�ĪŻĄ╚č³╚²ĮŪą╬Ą─īW┴ĢąĶę¬Å─Č©┴xĪóąį┘|║═┼ąČ©╚²ĘĮ├µ╚źīW┴Ģ║═šŲ╬š��Ż¼Ą╚č³╚²ĮŪą╬Ą─╚²ŠĆ║Žę╗ąį┘|╩Ū┐╝įć▒ž┐╝Ą─ā╚╚▌��Ż¼┤╦═Ō��Ż¼į┌Ą╚č³╚²ĮŪųąę╗Č©ę¬ėąĘųŅÉėæšōęŌūR����Ż¼Ž±į┌ę╗ą®ėąĻPĄ╚č³╚²ĮŪą╬Ą─Äū║╬ŠC║ŽŅ}ųąŻ¼Įø(j©®ng)│ŻąĶę¬▀\ė├ĘųŅÉėæšō╦╝Žļ��ĪŻ

5����ĪóĄ╚▀ģ╚²ĮŪą╬ĪŻĄ╚▀ģ╚²ĮŪą╬╩Ū╠ž╩ŌĄ─Ą╚č³╚²ĮŪą╬�Ż¼Š▀ėąĄ╚č³╚²ĮŪą╬╦∙ėąĄ─ąį┘|Ż¼Ūę╚²▀ģČ╝ŽÓĄ╚����Ż¼╚²ĮŪČ╝×ķ60°����Ż¼į┌┐╝įćųąĮø(j©®ng)│ŻĢ■┐╝ĄĮŲõąį┘|�ĪŻ


6Īóų▒ĮŪ╚²ĮŪą╬����ĪŻī”ė┌ų▒ĮŪ╚²ĮŪą╬Ą─īW┴ĢąĶ꬚Ų╬šÄū┤¾ēKų¬ūR³cŻ¼ų▒ĮŪ╚²ĮŪą╬Ą─ąį┘|��Īóų▒ĮŪ╚²ĮŪą╬Ą─┼ąČ©╝░│§ųąÄū║╬ūŅųžę¬Ą─Č©└Ē╣┤╣╔Č©└Ē����Ż¼ī”ų▒ĮŪ╚²ĮŪą╬Ą─╦∙ėąĄ─ąį┘|Č©└Ē║═┼ąČ©Č╝▒žĒÜę¬╩ņŠÜšŲ╬šŻ¼Ž±ų▒ĮŪ╚²ĮŪą╬ą▒▀ģ╔ŽĄ─ųąŠĆĄ╚ė┌ą▒▀ģĄ─ę╗░ļ▀@ŚlČ©└Ēį┌┐╝įćųąĮø(j©®ng)│�Ż┐╝ĄĮ��Ż¼Ą½╚▌ęū▒╗īW╔·╦∙║÷ęĢ����ĪŻ
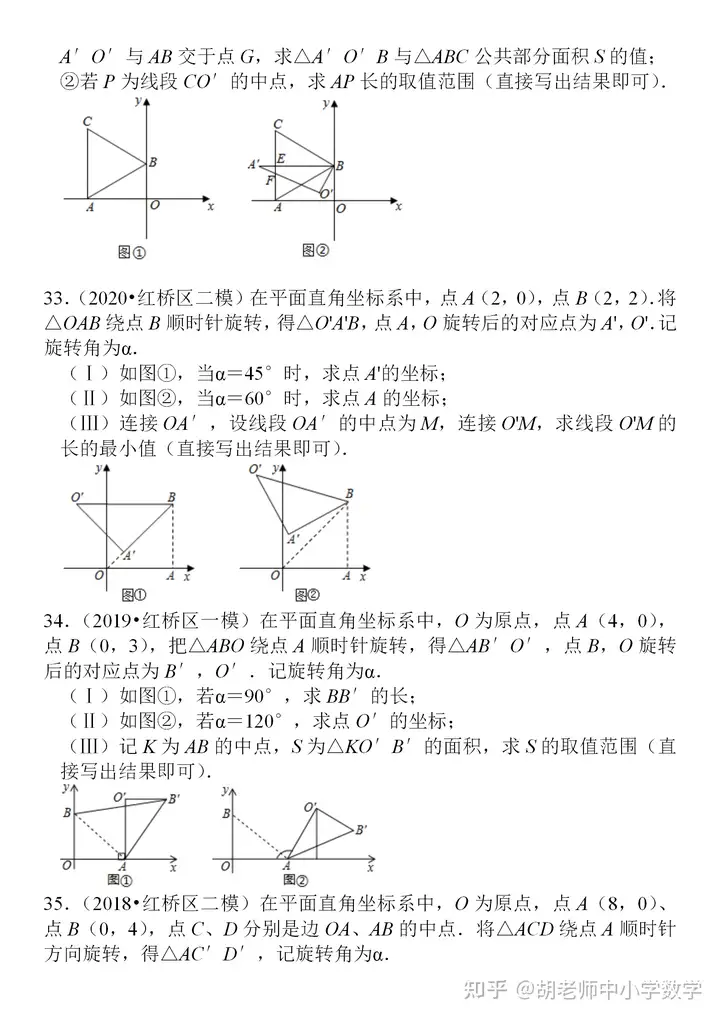
│²┤╦ų«═Ō▀ĆąĶšŲ╬šā╔ųą╠ž╩ŌĄ─╚²ĮŪą╬(║¼ėą45Č╚Ą─ų▒ĮŪ╚²ĮŪą╬║═║¼ėą30Č╚Ą─ų▒ĮŪ╚²ĮŪą╬)Ą─ąį┘|Ż¼į┌ĮŌŅ}ųąĮø(j©®ng)│ŻąĶę¬▀\ė├ĄĮ▀@ā╔ĘN╚²ĮŪą╬Ą─ąį┘|�Ż¼Ž±Įø(j©®ng)│Żų▒Įėė├į┌ų▒ĮŪ╚²ĮŪą╬ųą30°╦∙ī”Ą─ų▒ĮŪ▀ģ╩Ūą▒▀ģĄ─ę╗░ļ▀@Śląį┘|ėŗ╦Ńų▒ĮŪ╚²ĮŪą╬Ą─▀ģķLĪŻ
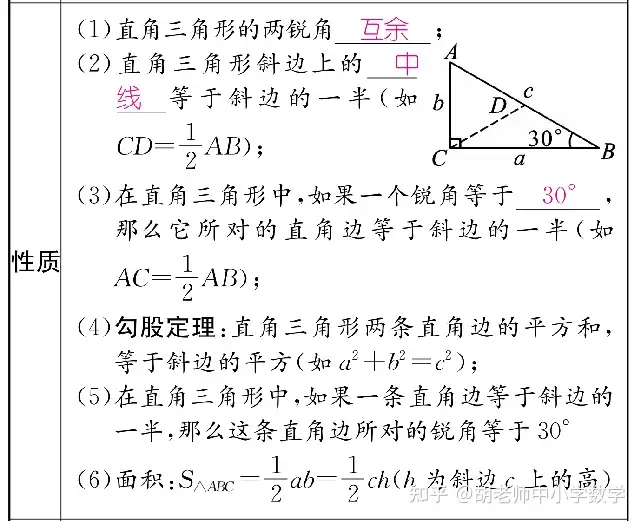

7����ĪóŽÓ╦Ų╚²ĮŪą╬����ĪŻŽÓ╦Ų╚²ĮŪą╬Ą─ąį┘|╝░Ųõ┼ąČ©╩ŪīW┴ĢĄ─ųž³c����Ż¼ŽÓ╦Ų╚²ĮŪą╬Īó╚½Ą╚╚²ĮŪą╬╝░õJĮŪ╚²ĮŪą╬║»öĄ(sh©┤)ū„×ķ╚²ĮŪą╬Ą─╚²┤¾╣żŠ▀�Ż¼į┌ĮŪČ╚ėŗ╦ŃĪó▀ģķLėŗ╦Ń╝░▀ģĮŪĻPŽĄĄ─ūC├„╔ŽėąĘŪ│ŻÅVĘ║Ą─ė├╠Ä��Ż¼ŽÓī”╚½Ą╚╚²ĮŪą╬����Ż¼ŽÓ╦Ų╚²ĮŪą╬Ą─ļyČ╚Ģ■┬į┤¾ę╗ą®Ż¼į┌ųą┐╝Ģ■ų▒Įė┐╝▓ķĄĮ└¹ė├ŽÓ╦Ų£yĖ▀╗“ėŗ╦ŃŠĆČ╬ķLČ╚�Ż¼ę▓Ģ■į┌╦─▀ģą╬ĪółAęį╝░Äū║╬ŠC║ŽŅ}ųą┐╝▓ķĄĮŽÓ╦Ų��ĪŻ
8�ĪóõJĮŪ╚²ĮŪą╬║»öĄ(sh©┤)Ż¼ī”õJĮŪ╚²ĮŪ║»öĄ(sh©┤)Ą─īW┴Ģ����Ż¼ąĶ꬚Ų╬š╚²ĘNõJĮŪ╚²ĮŪ║»öĄ(sh©┤)Ą─Č©┴x����Īó╠ž╩ŌĄ─╚²ĮŪ║»öĄ(sh©┤)ųĄ╝░õJĮŪ╚²ĮŪ║»öĄ(sh©┤)Ą─æ¬ė├�Ż¼ŲõųąČ©┴x╝░╠ž╩ŌĄ─╚²ĮŪ║»öĄ(sh©┤)ųĄ╩Ū╗∙ĄAŻ¼æ¬ė├╩Ūųž³c����ĪŻ

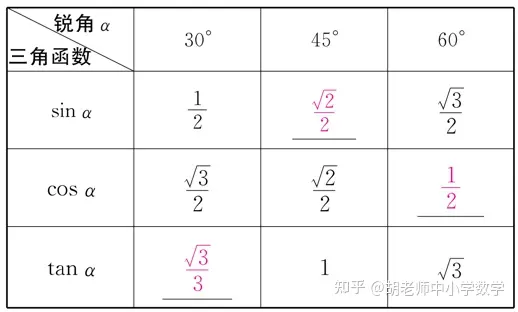
╚²ĮŪą╬ū„×ķųą┐╝▒ž┐╝Ą─ų¬ūR³cŻ¼į┌┐╝Ņ}╔Ž╝╚ėą╠žäe╗∙ĄAĄ─Ņ}�Ż¼ę▓ėąųąĄ╚Ņ}Ż¼▀Ćėąę╗ą®ŠC║ŽŅ}����Ż¼į┌Å═┴Ģéõ┐╝Ą─▀^│╠ųą╩ūŽ╚ąĶ꬚Ų╬šų¬ūRę¬³c║═╝Ü╣Ø(ji©”)Ż¼┴╦ĮŌ┐╝³c��Īó┐╝Ž“║═Ņ}ą═�Ż¼į┘Äū║╬ūį╔ĒŪķør╚źū÷ę╗ą®ėąßśī”ąįĄ─ŠÜ┴ĢŅ}ĪŻ
ĘųŽĒę╗Ę▌▒╚▌^Įø(j©®ng)ĄõĄ─╚²ĮŪą╬ŠÜ┴ĢŅ}��Ż¼▀@ą®Ņ}─┐Š∙üĒūįĮ³╚²─Ļ─│ĄžĖ„ąŻĄ──����Ż┐╝įćŠĒŻ¼─├ĄĮŅ}─┐║¾╬ęūį╝║ę▓═Ļš¹ū÷┴╦ę╗▒ķ����Ż¼░l(f©Ī)¼F(xi©żn)▀@Ę▌Ņ}─┐┘|┴┐▌^Ė▀Ż¼Äū║╬║Ł╔w┴╦╚²ĮŪą╬Ą─╦∙ėą║╦ą─┐╝³c║═Ņ}ą═��Ż¼ę▓░³║¼ų°ę╗ą®│ŻęŖĄ──Żą═�Ż¼║▄ČÓŅ}─┐▀Ć╩ŪŠ▀ėąę╗Č©Ą─ŠC║Žąį║═ļyČ╚Ż¼▀m║Ž╗∙ĄAųąĄ╚╝░Ų½╔ŽĄ─īW╔·╚źŠÜ┴Ģ����Ż¼ė╚Ųõ╩ŪĮŌ┤Ņ}Ą─Ą┌╚²å¢Ż¼║▄ČÓČ╝ę¬Ū¾ų▒Įėīæ│÷┤░Ė�Ż¼Ą½ø]ėąš²┤_Ą─╦╝┬Ę║══Ļš¹Ą─▀^│╠ėųį§Ģ■ėąš²┤_Ą─┤░Ė─ž?Ą┌╚²å¢┤¾▓┐ĘųČ╝╩ŪÄū║╬ŠC║Ž╠ĮŠ┐Ņ}Ż¼╔µ╝░ĄĮĘŁš█�Īóą²▐DĄ╚łDą╬Ą─ūā╗»Ż¼łDŽ±Ė³╝ė│ķŽ¾��Ż¼║▄ČÓĢr║“ąĶę¬ūį╝║╚źū„łD��ĪóĘų╬÷��Ż¼╚╗║¾īżšęĮŌŅ}╦╝┬Ę║═ĘĮĘ©��Ż¼▀@ą®Ņ}─┐▀m║Ž╗∙ĄA▒╚▌^į·īŹĄ─ę╗ą®═¼īWüĒ═Ļ│╔��ĪŻ

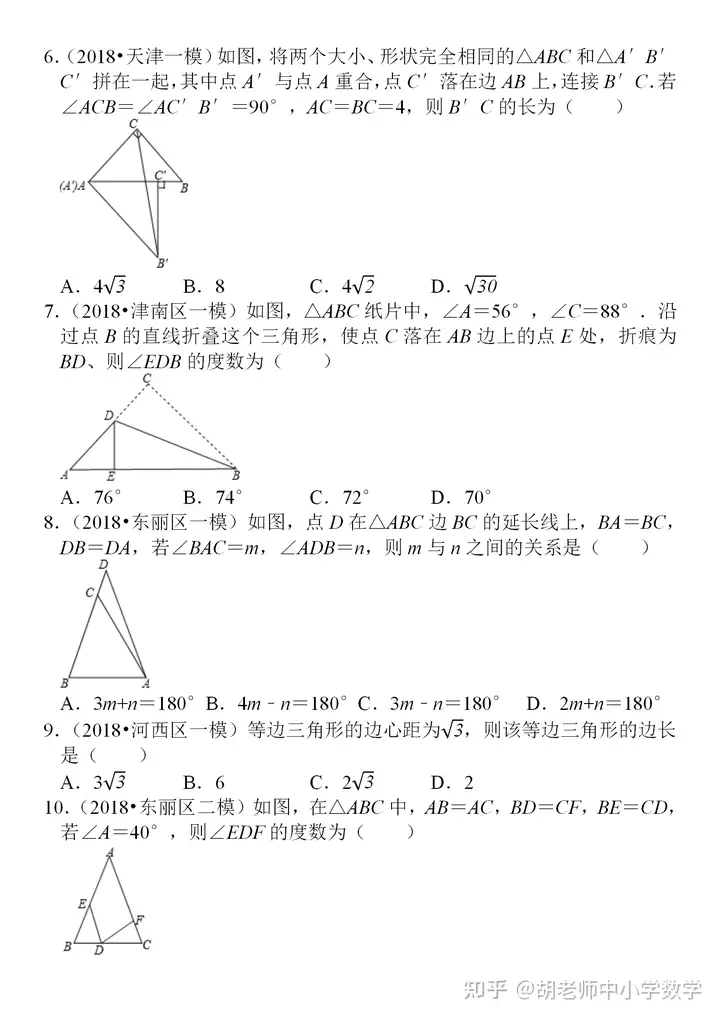

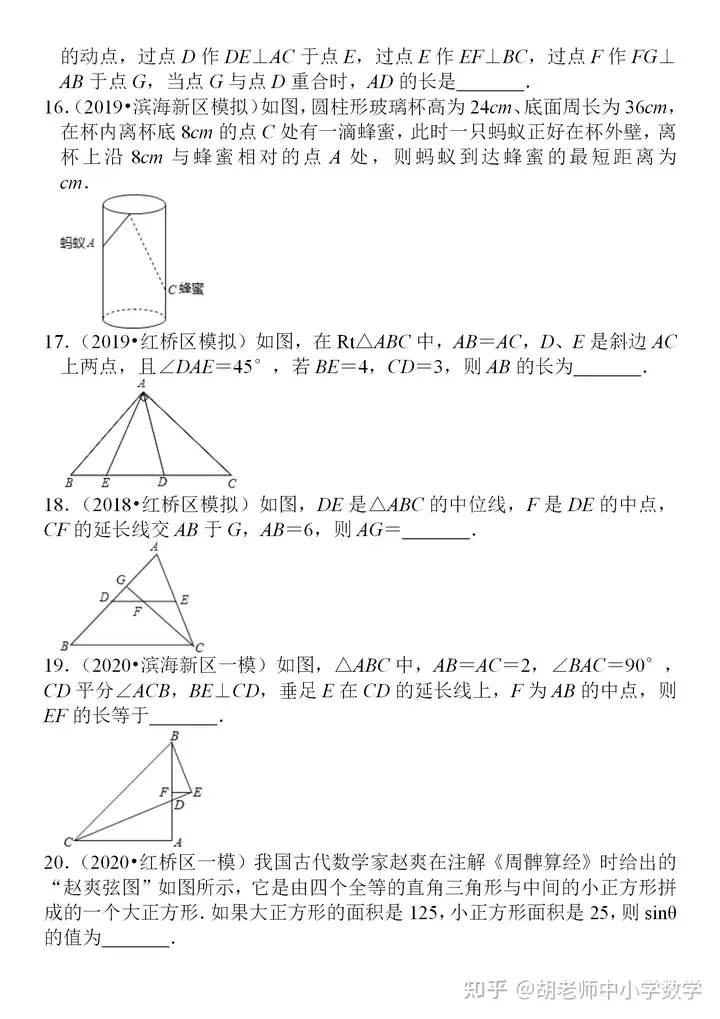



























ŠÄ▌ŗ═Ų╦]Ż║
2023─Ļųą┐╝Ė„┐Ų─┐ųž³cų¬ūRģR┐é
ĪĪĪĪūŅą┬ųą┐╝┘YėŹĪóųą┐╝š■▓▀����Īó┐╝Ū░£╩éõĪóųą┐╝ŅA£y����Īóõø╚ĪĘųöĄ(sh©┤)ŠĆĄ╚
ĪĪĪĪųą┐╝ĢrķgŠĆĄ─╚½▓┐ųžę¬╣Ø(ji©”)³c
ĪĪĪĪ▒Mį┌"ųą┐╝ŠW(w©Żng)"╬óą┼╣½▒Ŗ╠¢

ĪĪĪĪ ÜgėŁ╩╣ė├╩ųÖCĪóŲĮ░ÕĄ╚ęŲäėįOéõįLå¢ųą┐╝ŠW(w©Żng)��Ż¼2023ųą┐╝ę╗┬Ę┼Ń░ķ═¼ąą����ŻĪ>>³cō¶▓ķ┐┤






















































