Å═┴Ģ
Å═┴Ģ╩ŪéĆ║├┴ĢæT�Ż¼į┌▀Mąą▒ŠŲ¬ā╚(n©©i)╚▌ų«Ū░╬ęéāŽ╚╗žæø╔Žę╗Ų¬ā╚(n©©i)╚▌Ą├│÷Ą─ĮY(ji©”)šōŻ║(▀ĆųĖ═¹╬ęš│┘NÅ═ųŲå߯¼«ö╚╗ę¬─Ń▒│└▓)
Å═┴Ģ═Ļ«ģŻ¼ķ_╩╝š²Ņ}
1.ĮŌ╬÷╩ĮĄ─ė╔üĒ
╔Žę╗Ų¬Ą─ā╚(n©©i)╚▌�Ż¼Ä═╬ęéāĮ©┴ó┴╦Äū║╬ė^─Ņ╔ŽĄ─║»öĄ(sh©┤)╝┤Ż║║»öĄ(sh©┤)╩ŪŠĆĪŻų╗ėąÄū║╬ė^─Ņ����Ż¼ī”ė┌║»öĄ(sh©┤)üĒųv╩Ū═Ļ╚½▓╗ē“Ą─Ż¼ī┘ė┌╚▒Ėņ▓▓╔┘═╚����Ż¼▓╗═Ļš¹ĪŻöĄ(sh©┤)īWöĄ(sh©┤)īW����Ż¼ø]ėą┤·öĄ(sh©┤)Š═ø]ėąņ`╗ĻŻ¼╦∙ęįĮ±╠ņ╬ęéāüĒ░č╦³Ą─ņ`╗ĻĮo╦³čb▀M╚ź����ĪŻ«ģŠ╣╩Ūę¬čbņ`╗Ļ┬’Ż¼╩ŪéĆ╝╝ąg╗Ņ��Ż¼─ŪŠ═Ž╚─├ūŅ║åå╬Ą─ŠÜŠÜ╩ų����Ż¼ę▓Š═╩Ūę╗┤╬║»öĄ(sh©┤)��Ż¼┐┤┐┤╦³Ą─▄|Üż
Óµ�Ż¼╗©└’║·╔┌�Ż¼üyŲ▀░╦įŃĪŻŽ╚─├ę╗éĆ│÷üĒ�Ż¼ė├Ę┼┤¾ńR┐┤ę╗Ž┬
Ó┼Ż¼ėą─Ū├┤³cā║ęŌ╦╝┴╦��Ż¼įŁüĒ║»öĄ(sh©┤)ŠĆšµĄ─╩Ūė╔ū°ś╦³cĮM│╔Ą─����Ż¼╬ęéā╔Žę╗Ų¬Ą─└ĒšōŠ═▒╗īŹÕN┴╦ĪŻ▀@³c▒╗īŹÕN┴╦��Ż¼─Ū╩Ū▓╗╩ŪŠ═┐╔ęį▀@śė└ĒĮŌ║»öĄ(sh©┤)Ą─┤·öĄ(sh©┤)╗»=ū°ś╦³cĄ─┤·öĄ(sh©┤)╗»��ĪŻČ°Ūę��Ż¼ĘŪ│ŻŪ╔Ą─╩Ū��Ż¼├┐ę╗éĆū°ś╦³cČ╝ėąų°ŽÓī”æ¬Ą─ÖMū°ś╦║═┐vū°ś╦üĒ▒Ē▀_Ųõ╔ĒĘ▌Ąž╬╗�Ż¼ÖMū°ś╦Īó┐vū°ś╦ėųäé║├╩ŪöĄ(sh©┤)ūųĪŻ╠O╣¹Č╝įęĄĮ─ŃŅ^╔Ž┴╦��Ż¼Ž┬ę╗▓Įįōį§├┤▐k▓╗ė├╬ęČÓšf┴╦░╔��Ż¼«ö╚╗╩Ū░č╦³éā┴ą│÷üĒ║├║├ė^▓ņ░Ī����ĪŻ
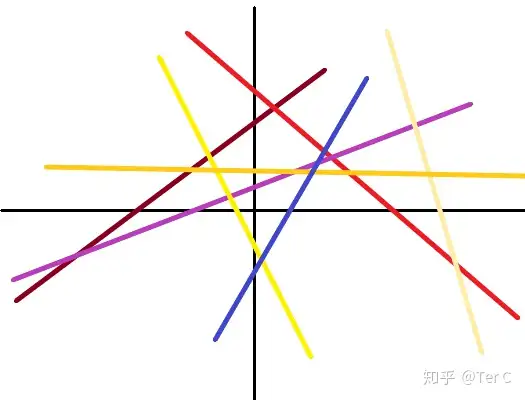
(5Ż¼9)(4�Ż¼6)(3��Ż¼3)(2�Ż¼0)(1Ż¼-3)(0����Ż¼-6)(-1Ż¼-9)
ė^▓ņ═Ļ«ģ║¾����Ż¼░┤šš┼ŻŅDĄ─ū÷Ę©Ż¼─Ń╩Ū▓╗╩ŪŠ═Žļå¢Ż║×ķ╩▓├┤▀@ą®³cį┌ę╗Ślų▒ŠĆ╔Ž?╚╗║¾╬ęŠ═Žļę╗Ę█╣PŅ^įę─ŃŅ^╔Ž����Ż¼═³┴╦Ū░ę╗Ų¬Ą─ā╚(n©©i)╚▌┴╦?ę“×ķ╦³éāėąęÄ(gu©®)┬╔░Ī!!!╝╚╚╗╩ŪęÄ(gu©®)┬╔Ż¼─ŪŠ═╩Ūūā╗»Ż¼╩Ūūā╗»░┤šš╬ęéāĄ─═©ė├ĮŌĘ©����Ż¼Ž╚üĒéĆ║¾├µĄ─£pŪ░├µĄ─ĪŻ▀@└’╩Ūū°ś╦³c����Ż¼╦∙ęį╬ęéāŠ═║¾├µĄ─ÖMū°ś╦£pŪ░├µĄ─ÖMū°ś╦Ż¼┐vū°ś╦═¼└Ē����ĪŻ
Ž╚üĒÖMū°ś╦
4-5=-1
3-4=-1
2-3=-1
1-2=-1
┐╔ų¬Č╝Ą╚ė┌-1
į┘üĒ┐vū°ś╦
6-9=-3
3-6=-3
0-3=-3
-3-0=-3
┐╔ų¬Č╝Ą╚ė┌-3
┐┤│÷Ą└Ą└┴╦┬’Ż¼Ę┤š²╬ę┐┤│÷üĒ┴╦��Ż¼─ŪŠ═╩Ūį┌ŽÓÓÅū°ś╦³cų«ķg��Ż¼ÖMū°ś╦£p1����Ż¼┐vū°ś╦ę¬£p3Ż¼Ę┤▀^üĒÖMū°ś╦╝ė1�Ż¼┐vū°ś╦ę¬╝ė3ĪŻ▀@ĄĮĄūī”▓╗ī”─ž��Ż¼▓╗Ę┴ū÷ę╗Ž┬“×ūC�Ż¼░┤šš▀@éĆ╦╝┬Ę����Ż¼Ęųäešę│÷(5����Ż¼9)Ū░├µĄ─ū°ś╦³c║═(-1Ż¼-9)║¾├µĄ─ū°ś╦³c����ĪŻ(5Ż¼9)Ū░├µū°ś╦³cĄ─ÖMū°ś╦×ķ6��Ż¼Å─5ĄĮ6ÖMū°ś╦╝ė1����Ż¼─Ū┐vū°ś╦╝ė3╝┤³c(6�Ż¼9)═¼└Ē┐╔Ą├(-1Ż¼-9)║¾├µĄ─ū°ś╦³c×ķ(-2��Ż¼-12)�Ż¼├Ķ³c▀BŠĆ
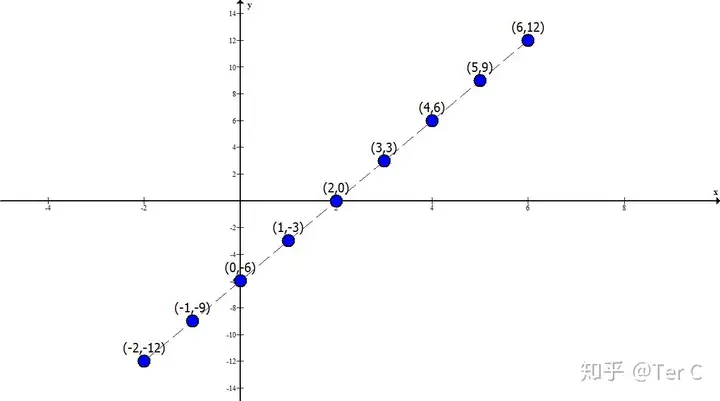
║▄├„’@Ż¼ą┬Ą├│÷Ą─³c║═įŁüĒĄ─³c╩Ūį┌ę╗Ślų▒ŠĆ╔Ž�Ż¼ūC├„╬ęéāĄ├ĄĮĄ─ęÄ(gu©®)┬╔╩Ūø]ėąÕeĄ─ĪŻ╝╚╚╗ŽÓÓÅū°ś╦³cų«ķg��Ż¼ėąų°ÖMū°ś╦£p1Ż¼┐vū°ś╦ę¬£p3����Ż¼Ę┤▀^üĒÖMū°ś╦╝ė1Ż¼┐vū°ś╦ę¬╝ė3▀@śėĄ─ęÄ(gu©®)┬╔�Ż¼╩Ū▓╗╩ŪŠ═╚f╩┬┤¾╝¬┴╦─ž?’@╚╗▓╗╩ŪŻ¼▒╚╚ń�Ż¼šł─Ńšę│÷(-2Ż¼-12)ų«║¾Ą─Ą┌50éĆū°ś╦³c�ĪŻ─Ū─ŃžM▓╗╩Ūę¬ųžÅ═╔Ž├µĄ─ū÷Ę©50▒ķ?50▒ķ─Ńšf─ŃąąŻ¼║├����Ż¼─Ūšłå¢Ą┌2020éĆ─ž?─Ń▀Ćšf─ŃąąŻ¼╬ęį┘å¢Ą┌20102949203éĆ─ž?▓╗ąą┴╦░╔����ĪŻtoo young too simpleĪŻ▀@Š═šf├„╬ęéāĄ├ĄĮĄ─ęÄ(gu©®)┬╔▓╗ē“Ųš▒ķ�Ż¼▓╗ūŃęįė├ė┌ėŗ╦ŃŻ¼ąĶę¬└^└m(x©┤)═ŲÅV╗»�ĪŻ

╬ęéāį┌ąĪīWČ■─Ļ╝ēīW▀^╝ė£pĘ©Ą─═ŲÅV▀\╦Ń╩Ū│╦│²Ę©Ż¼╬ęéāŠ═░čęÄ(gu©®)┬╔┐éĮY(ji©”)×ķ│╦│²Ą─ęÄ(gu©®)┬╔╝┤┐vū°ś╦Ą─į÷╝ė┴┐╩ŪÖMū°ś╦į÷╝ė┴┐Ą─3▒Č��ĪŻŽ╚“×ūCę╗Ž┬Ę¹▓╗Ę¹║ŽįŁüĒĄ─▒╚╚ń(5�Ż¼9)║═(2�Ż¼0)ė├ę╗Ž┬ą┬Ą├ĄĮĄ─ęÄ(gu©®)┬╔
Å─5ĄĮ2į÷╝ė┴╦-3��Ż¼┐vū°ś╦Š═ę¬į÷╝ė-9����Ż¼9+(-9)=0Ż¼bingoš²┤_����ĪŻ
║¾Ą─Ą┌50éĆū°ś╦³cį┘ėŗ╦Ń(-2Ż¼-12)ų«║¾Ą─Ą┌50éĆū°ś╦³c
į┌-2║¾├µ��Ż¼ėų╩ŪĄ┌50éĆ��Ż¼╦∙ęįÖMū°ś╦=-52����Ż¼Ė∙ō■(j©┤)ęÄ(gu©®)┬╔ėą┐vū°ś╦=-12-50*3=-162
═¼└Ē┐╔ėŗ╦Ń╚╬ęŌū°ś╦³c
ė^▓ņėŗ╦Ń▀^│╠┐╔ų¬����Ż¼ėŗ╦Ń▒ŠŚlų▒ŠĆĄ─╚╬ęŌū°ś╦³cŻ¼ąĶę¬ė├ĄĮ╬ęéāĄ─ęÄ(gu©®)┬╔║═ę╗éĆęčų¬ū°ś╦³c����ĪŻ
ØMūŃė┌▒ŠŚlų▒ŠĆū°ś╦³cĄ─ęÄ(gu©®)┬╔šęĄĮ┴╦��Ż¼äe═³┴╦╬ęéāĄ─ūŅĮK─┐ś╦Ż║ęÄ(gu©®)┬╔┤·öĄ(sh©┤)╗»�ĪŻ╬ęéā?n©©i)╬ęŌĮo│÷▒ŠŚlų▒ŠĆ╔Žę╗ū°ś╦³c(x�Ż¼y)Ż¼▀x╚Ī(5��Ż¼9)×ķ╗∙£╩ū°ś╦³c��ĪŻ
┐vū°ś╦Ą─į÷╝ė┴┐
y-9
ÖMū°ś╦Ą─į÷╝ė┴┐
x-5
┐vū°ś╦Ą─į÷╝ė┴┐╩ŪÖMū°ś╦į÷╝ė┴┐Ą─3▒Č
y-9=3*(x-5)
Ą├y=3x-6
╦∙ęįy=3x-6┤·▒Ē┴╦▒ŠŚlŠĆĄ─╦∙ėąū°ś╦³c�Ż¼▀MČ°┤·▒Ē┴╦▒ŠŚlų▒ŠĆ
▀Ćø]═ĻŻ¼▀@ŚlŠĆ╩Ū3▒Č��Ż¼─Ūėąø]ėą4▒Č�Ż¼5▒ČŻ¼6▒Č��Ż¼┐ŽČ©╩ŪėąĄ─��Ż¼╦∙ęį╬ęéāŠ═┴Ņk=╚╬ęŌ│ŻöĄ(sh©┤)�Ż¼Ēś└Ē│╔š┬Ą─Š═░č▀@éĆęÄ(gu©®)┬╔═ŲÅVĄĮ┴╦╦∙ėąę╗┤╬║»öĄ(sh©┤)ŠĆ╝┤į┌ę╗┤╬║»öĄ(sh©┤)ŠĆųąŻ¼┐vū°ś╦Ą─į÷╝ė┴┐╩ŪÖMū°ś╦į÷╝ė┴┐Ą─k▒ČĪ�Ż¼F(xi©żn)į┌ę¬═Ļ│╔▀@ŚlęÄ(gu©®)┬╔┤·öĄ(sh©┤)╗»Ż¼ęį▒Ē▀_╦∙ėąĄ─ę╗┤╬║»öĄ(sh©┤)ŠĆ����ĪŻęčų¬ę╗Ślę╗┤╬║»öĄ(sh©┤)ŠĆ����Ż¼┐vū°ś╦Ą─į÷╝ė┴┐╩ŪÖMū°ś╦į÷╝ė┴┐Ą─k▒Č����Ż¼ęčų¬ū°ś╦³c(mŻ¼n)����Ż¼Ū¾╚╬ęŌū°ś╦³c(xŻ¼y)��ĪŻ
┐vū°ś╦Ą─į÷╝ė┴┐
y-n
ÖMū°ś╦Ą─į÷╝ė┴┐
x-m
┐vū°ś╦Ą─į÷╝ė┴┐╩ŪÖMū°ś╦į÷╝ė┴┐Ą─k▒Č
y-n=k*(x-m)
y=kx+n-km(┐┤ŲüĒ╠½Å═ļs▓╗ŪÕ╦¼)
▓╗Ę┴┴Ņb=n-km
╦∙ęįy=kx+b
┤¾╣”Ėµ│╔y=kx+bŠ═╩Ū╦∙ėąę╗┤╬║»öĄ(sh©┤)ŠĆĄ─┤·▒Ē
ū÷┴╦▀@├┤ČÓĄ─╣żū„��Ż¼ĮKė┌░čę╗┤╬║»öĄ(sh©┤)Å─ų▒ŠĆūā│╔┴╦y=kx+b▀@śėę╗Śl┤·öĄ(sh©┤)╩Į�Ż¼ėų╩ŪŪ¾ĮŌėų╩ŪĘų╬÷Ą─Ż¼Įo▀@Śl┤·öĄ(sh©┤)╩ĮŲéĆ├¹ūų░╔Š═ĮąĮŌ╬÷╩Į��ĪŻÄū║╬ĘĮ├µĄ─ę╗┤╬║»öĄ(sh©┤)Č╝ėąČ©┴x����Ż¼┤·öĄ(sh©┤)ĘĮ├µĄ─ūį╚╗▓╗─▄╔┘�Ż¼ĮY(ji©”)║Žęį╔Žā╚(n©©i)╚▌Š═╩Ūę╗┤╬║»öĄ(sh©┤)Ą─Č©┴xą╬╚ńy=kx+b(kŻ¼b×ķ│ŻöĄ(sh©┤)����Ż¼k≠0)��Ż¼Ųõųąx×ķūįūā┴┐y×ķę“ūā┴┐��Ż¼Įąū÷ę╗┤╬║»öĄ(sh©┤)
└ŽęÄ(gu©®)Šž┐éĮY(ji©”)ę╗Ž┬

perfect��Ż¼ĮėŽ┬üĒ┐┤ąį┘|(zh©¼)

2.ŽÓĻPąį┘|(zh©¼)
šfĄĮąį┘|(zh©¼)�Ż¼▒ž╚╗Š═╩Ū┐╝▓ņĄ─ųž³c����Ż¼ę▓Š═╩Ū═┤³c┴╦Ż¼į§├┤▓┼─▄░čąį┘|(zh©¼)ėø║├?╬╣����Ż¼▀@╩ŪöĄ(sh©┤)īWÜGŻ¼«ö╚╗╩Ūę¬└ĒĮŌėøæøūŅ║├┴╦░Ī����ĪŻ─Ū╬ęę¬└ĒĮŌšl─ž?╬╣Ż¼ĮŌ╬÷╩ĮČ╝Įo─Ń┴╦��Ż¼─Ń┐┤░Ī�Ż¼y=kx+bŻ¼«ö╚╗╩Ū└ĒĮŌk║═bį§├┤ė░Ēæ║»öĄ(sh©┤)┴╦░Ī
kųĄį§├┤ė░Ēæ║»öĄ(sh©┤)
Å─Č©┴x└’╬ęéāų¬Ą└k=╚╬ęŌ│ŻöĄ(sh©┤)Ż¼╬ęéāį┌ąĪīWČ■─Ļ╝ēīW▀^öĄ(sh©┤)╩Ūėą┤¾ąĪėąš²žōĄ─����Ż¼Š═Å─▀@ā╔éĆĘĮ├µüĒ┐┤kųĄī”ė┌ę╗┤╬║»öĄ(sh©┤)ŠĆĄ─ė░ĒæĪŻ
(1)š²žō
į┌蹊┐kųĄ����Ż¼Ė∙ō■(j©┤)┐žųŲūā┴┐Ę©Ż¼ąĶ▒Ż│ųbųĄ▓╗ūā�Ż¼Ė╔┤Óę╗³cų▒Įėūīb=0ĪŻ┴ąÄūéĆkųĄš²žō▓╗═¼Ą─ĮŌ╬÷╩Į��Ż¼╚╗║¾ū„łDė^▓ņ
y=2x | y=4x | y=12x | y=-2x | y=-8x | y=-12x
ū„łD┴„│╠Ż║Ū¾³cū°ś╦����Īó├Ķ³cĪó▀BŠĆ
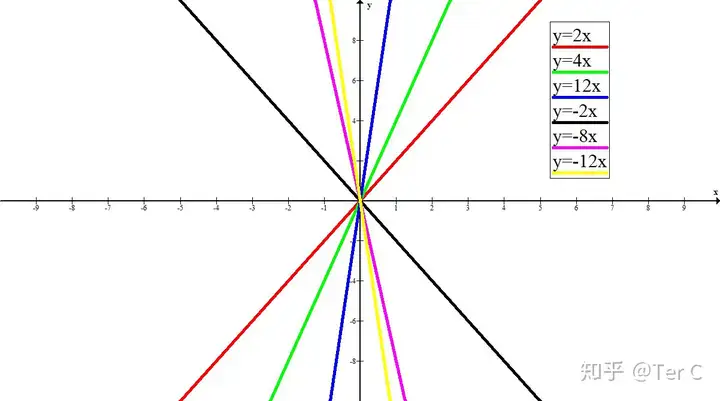
┐┤łD║▄╚▌ęū░l(f©Ī)¼F(xi©żn)
k>0Ą─ę╗┤╬║»öĄ(sh©┤)��Ż¼łDŽ±Č╝Įø(j©®ng)▀^Ą┌ę╗��ĪóĄ┌╚²Ž¾Ž▐
k<0Ą─ę╗┤╬║»öĄ(sh©┤)��Ż¼łDŽ±Č╝Įø(j©®ng)▀^Ą┌Č■����ĪóĄ┌╦─Ž¾Ž▐
ė╔┤╦┐╔ų¬kųĄĄ─š²žōė░Ēæų°ę╗┤╬║»öĄ(sh©┤)ū°ś╦³cĄ─Ęų▓╝
kĄ─š²žō▓╗═¼yļSxĄ─ūā╗»Ūķørę▓▓╗═¼
(2)┤¾ąĪ
蹊┐ĘĮĘ©═¼╔ŽŻ¼▀Ć╩Ū╦³éāÄūéĆ
y=2x | y=4x | y=12x | y=-2x | y=-8x | y=-12x
ū„łD┴„│╠Ż║Ū¾³cū°ś╦Īó├Ķ³c��Īó▀BŠĆ

┐╔ęį┐┤ĄĮ╝t����ĪóŠG����Īó╦{╚²ŚlŠĆĄ─kųĄĘųäe×ķ2Īó4��Īó12��Ż¼║▄╚▌ęū░l(f©Ī)¼F(xi©żn)
«ök>0Ģr
kųĄįĮ┤¾����Ż¼łDŽ±┼cx▌SŖAĮŪŠ═įĮ┤¾
łDŽ±┼cx▌SŖAĮŪė└▀hČ╝╩ŪõJĮŪ
«ök<0Ģr
kųĄįĮ┤¾Ż¼łDŽ±┼cx▌SŖAĮŪę▓╩ŪįĮ┤¾
łDŽ±┼cx▌SŖAĮŪė└▀hČ╝╩ŪŌgĮŪ
ę“┤╦kųĄėąéĆŅ~═ŌĘQ║¶ĮąŻ║ą▒┬╩
bųĄį§├┤ė░Ēæ║»öĄ(sh©┤)
Ė·kųĄĄ─蹊┐ĘĮĘ©ęŌ┴x����Ż¼Ą½╩Ū╬ęéā▓╗─▄ūīk=0Ż¼ę“×ķČ©┴x▓╗į╩įS��Ż¼ę“┤╦╬ęéā▒Ż│ųkųĄ▓╗ūā�ĪŻ┴ąÄūéĆkųĄŽÓ═¼bųĄ▓╗═¼Ą─┤¾╝ęė^▓ņę╗Ž┬Š═║├┴╦ĪŻ
y=2x+1 | y=2x+3 | y=2x+5 | y=2x-1 | y=2x-3 | y=2x-5
ū„łD
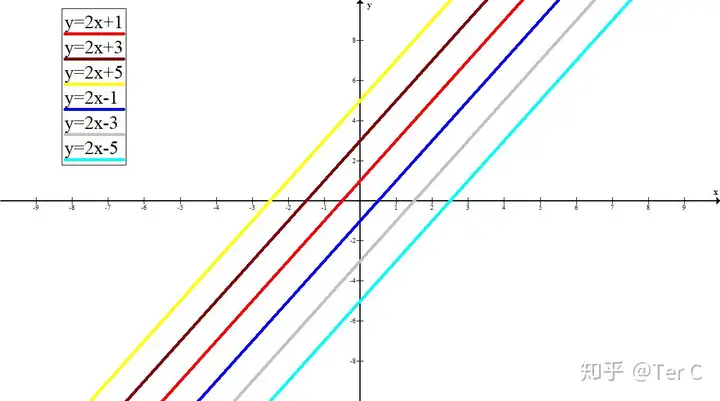
ę▓ĘŪ│Ż├„’@
b>0Ģr
łDŽ±┼cy▌SĮ╗ė┌y▌Sš²░ļ▌S
bųĄįĮ┤¾Ż¼┼cy▌SĮ╗³cįĮ┐┐╔Ž
b<0Ģr
łDŽ±┼cy▌SĮ╗ė┌y▌Sžō░ļ▌S
bųĄįĮąĪ��Ż¼┼cy▌SĮ╗³cįĮ┐┐Ž┬
▀Ć┐╔ęį░l(f©Ī)¼F(xi©żn)
kųĄŽÓ═¼����Ż¼ų▒ŠĆČ╝╩ŪŲĮąąĄ─
▀@ą®ų▒ŠĆČ╝┐╔ęįė├y=2xŽ“╔Ž╗“Ž“Ž┬ŲĮęŲŽÓæ¬éĆå╬╬╗Ą├ĄĮ
bųĄę▓ėąéĆŅ~═ŌĘQ║¶ĮąŻ║ĮžŠÓ
ąĪČ╬┐éĮY(ji©”)
3.ŽÓĻP┐╝³c
(1)łDŽ±┐╝▓ņ
#1ĮołDŽ±▒µäekųĄĪóbųĄš²žō┼c┤¾ąĪ(Įø(j©®ng)│Ż┼cŲõ╦³║»öĄ(sh©┤)ĮY(ji©”)║Ž)
#2ĮobųĄ��ĪókųĄ▒µäełDŽ±
#3łDŽ±īŹļHæ¬ė├(k>0��Ż¼Ą┌ę╗Ž¾Ž▐ā╚(n©©i))
įŁ└ĒŻ║xųĄŽÓ═¼��Ż¼kųĄįĮ┤¾�Ż¼yųĄįĮ┤¾
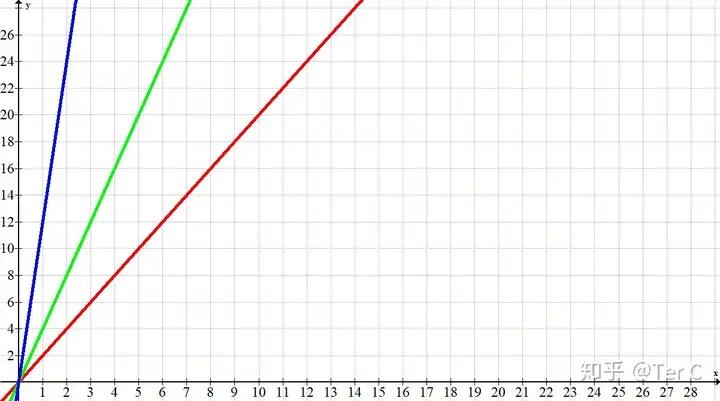
#4╚ńłD╦∙╩ŠŻ¼«öx=5Ģr��Ż¼yųĄ┤¾ąĪę└┤╬╩ŪŻ║╝tŠĆ<ŠGŠĆ<╦{ŠĆ
##┐╝▓ņĘĮ╩Į×ķ����Ż¼░čÖM┐vū°ś╦U/I╝┤×ķ│§╚²╬’└ĒļŖīWłDŽ±┐╝▓ņŻ¼ōQ│╔m/v╝┤×ķ│§Č■╬’└Ē┘|(zh©¼)┴┐┼c├▄Č╚łDŽ±┐╝▓ņ�Ż¼ōQ│╔F/V╝┤×ķ│§Č■ĖĪ┴”łDŽ±┐╝▓ņŻ¼═¼└Ē▀Ćėąv-tłD�Īós-tłDĄ╚Ą╚Ż¼ž×┤®│§Ė▀ųą╬’└Ē�Ż¼Ė▀ųą╬’└Ē▀Ć┐╔ęįė├łDŽ±ĮŌøQÅ═ļsä“╝ėä“£pĄ─╬╗ęŲå¢Ņ}
#5╗»īWę▓═¼└Ē┐╔ōQ
#6īWöĄ(sh©┤)īWĄ─═¼Ģr�Ż¼░č▀@├┤ČÓĄ─└Ē╗»å¢Ņ}Č╝īW┴╦��Ż¼╬ęŠ═å¢─ŃÉ█┴╦ø]ėą�ĪŻšµ╩ŪōņĄĮīÜ┴╦─žŻ¼╣■╣■╣■╣■╣■
(2)Ū¾ĮŌ╬÷╩Į
#1▀@éĆŅ}─┐Ą─įŁ└ĒŠ═╩Ūā╔³c┤_Č©ę╗Ślų▒ŠĆ
ų¬Ą└╚╬ęŌā╔³cū°ś╦����Ż¼┤·╚ļy=kx+b�Ż¼┐╔Ą├ĻPė┌kĪóbĄ─Č■į¬ę╗┤╬ĘĮ│╠����Ż¼ĮŌ│÷kĪóbŠ═┐╔ęį┴╦��Ż¼▓╗ČÓšf��ĪŻ▓╗Ģ■Š═╚źīWę╗Ž┬Č■─Ļ╝ēīW▀^Ą─ĮŌČ■į¬ę╗┤╬ĘĮ│╠
#2─Ńę▓┐╔ęįŽ╚Ū¾k��Ż¼į┘ė├╬ęĮ╠─ŃĄ─ėŗ╦ŃĘĮĘ©��Ż¼▓╗▀^▀Ć╩Ū═Ų╦]šn▒ŠĄ─ĮŌĘ©����Ż¼▀Ć─▄ŠÜ┴Ģę╗Ž┬ĮŌČ■į¬ę╗┤╬ĘĮ│╠
(3)ĮŌæ¬ė├Ņ}
#1ĻPµIį┌ė┌įO╬┤ų¬öĄ(sh©┤)����Ż¼┴ąĘĮ│╠����Ż¼Å═ļsę╗³cĄ─┐╔─▄ę¬ĮY(ji©”)║ŽłDŽ±Ż¼┐╝▓ņ“öĄ(sh©┤)ą╬ĮY(ji©”)║Ž”▀@éĆöĄ(sh©┤)īW╦╝Žļ
#2äė³cå¢Ņ}└’╚ń╣¹ĻPŽĄ╩Į×ķę╗┤╬║»öĄ(sh©┤)ĻPŽĄ����Ż¼ę¬ĮY(ji©”)║Ž╚ĪųĄĘČć·üĒŪ¾ĮŌ
(4)┼cŲõ╦³║»öĄ(sh©┤)ĮM│╔ŠC║Žå¢Ņ}
#1Ū¾├µĘe
#2Ū¾ķLČ╚
#3Ū¾ŽÓæ¬Ą─ūŅ┤¾ūŅąĪųĄŻ¼ę¬ĮY(ji©”)║Ž╚ĪųĄĘČć·üĒ┐┤
#4Ū¾ū°ś╦³c
(5)║»öĄ(sh©┤)┼cĘĮ│╠
#1ų╗ąĶę¬└ĒĮŌę╗³c��Ż¼«öy=0Ģr����Ż¼ę╗┤╬║»öĄ(sh©┤)Š═ūā│╔┴╦kx+b=0Ż¼ę▓Š═ūā│╔┴╦ę╗į¬ę╗┤╬ĘĮ│╠����ĪŻ
#2Å─┤·öĄ(sh©┤)īė├µ┐┤ū°ś╦³c(xŻ¼0)Ą─ÖMū°ś╦╩Ūī”æ¬ĘĮ│╠Ą─ĮŌ
#3Å─Äū║╬īė├µ┐┤ę╗┤╬║»öĄ(sh©┤)łDŽ±┼cx▌SĮ╗³c×ķę╗éĆĘĮ│╠³c����Ż¼└ĒĮŌ║├▀@└’ī”ė┌Č■┤╬║»öĄ(sh©┤)Ė∙Ą─└ĒĮŌ║▄ėąÄ═ų·
(6)║»öĄ(sh©┤)┼c▓╗Ą╚╩Į
#1▀@└’▀Ć╩Ū“öĄ(sh©┤)ą╬ĮY(ji©”)║Ž”╦╝ŽļĄ─æ¬ė├
#2▒╚╚ń2x+1>0Ż¼┐╔ęį┐┤│÷y=2x+1▀@éĆ║»öĄ(sh©┤)Ą─y>0����Ż¼ę▓Š═╩Ūx▌S╔ŽĘĮĄ─łDŽ±
#3╚ń2x+1>-3x+4����Ż¼┐╔ęį┐┤│╔y1=2x+1┼cy2=-3x+4▀@ā╔éĆ║»öĄ(sh©┤)łDŽ±Ą─▒╚▌^
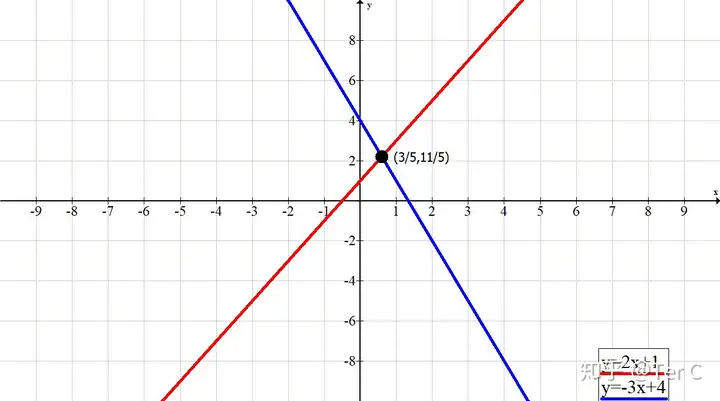
##Ą┌ę╗▓Į꬚ęĄĮĮ╗³c�Ż¼┐┤łD┐╔ų¬Į╗³cū°ś╦×ķ(3/5Ż¼11/5)
##ø]ėąĮ╗³cŠ═╩Ūø]ėąĮŌ
##Ą┌Č■▓Įę¬Ęųā╔▓┐Ęų┐┤��Ż¼Į╗³cū¾▀ģ║═Į╗³cėę▀ģ
##įōłD┐╔ų¬Į╗³cū¾▀ģ����Ż¼╦{ŠĆ“Tį┌╝tŠĆŅ^╔Ž����Ż¼╦∙ęį╩Ū2x+1<-3x+4ī”æ¬▓╗Ą╚╩ĮĄ─ĮŌ×ķx<3/5
##Į╗³cėę▀ģ╩Ū╝tŠĆ“Tį┌╦{ŠĆŅ^╔ŽŻ¼╦∙ęį╩Ū2x+1>-3x+4ī”æ¬▓╗Ą╚╩ĮĄ─ĮŌ×ķx>3/5
ĪĪĪĪ ÜgėŁ╩╣ė├╩ųÖC��ĪóŲĮ░ÕĄ╚ęŲäėįOéõįLå¢ųą┐╝ŠW(w©Żng)����Ż¼2023ųą┐╝ę╗┬Ę┼Ń░ķ═¼ąąŻĪ>>³cō¶▓ķ┐┤




















