(一)函數(shù)Update
1���、變量:在一個(gè)變化過(guò)程中可以取不同數(shù)值的量���。
常量:在一個(gè)變化過(guò)程中只能取同一數(shù)值的量。
2�����、函數(shù):一般的���,在一個(gè)變化過(guò)程中���,如果有兩個(gè)變量x和y,并且對(duì)于x的每一個(gè)確定的值�����,y都有唯一確定的值與其對(duì)應(yīng),那么我們就把x稱為自變量�����,把y稱為因變量���,y是x的函數(shù)���。
*判斷Y是否為X的函數(shù),只要看X取值確定的時(shí)候�,Y是否有唯一確定的值與之對(duì)應(yīng)
3、定義域:一般的���,一個(gè)函數(shù)的自變量允許取值的范圍���,叫做這個(gè)函數(shù)的定義域�����。
4�����、確定函數(shù)定義域的方法:
(1)關(guān)系式為整式時(shí),函數(shù)定義域?yàn)槿w實(shí)數(shù);
(2)關(guān)系式含有分式時(shí)�,分式的分母不等于零;
(3)關(guān)系式含有二次根式時(shí),被開(kāi)放方數(shù)大于等于零;
(4)關(guān)系式中含有指數(shù)為零的式子時(shí)�,底數(shù)不等于零;
(5)實(shí)際問(wèn)題中,函數(shù)定義域還要和實(shí)際情況相符合���,使之有意義�。
5���、函數(shù)的解析式:用含有表示自變量的字母的代數(shù)式表示因變量的式子叫做函數(shù)的解析式
6���、函數(shù)的圖像
一般來(lái)說(shuō),對(duì)于一個(gè)函數(shù)���,如果把自變量與函數(shù)的每對(duì)對(duì)應(yīng)值分別作為點(diǎn)的橫�����、縱坐標(biāo)�����,那么坐標(biāo)平面內(nèi)由這些點(diǎn)組成的圖形�,就是這個(gè)函數(shù)的圖象.
7、描點(diǎn)法畫函數(shù)圖形的一般步驟
第一步:列表(表中給出一些自變量的值及其對(duì)應(yīng)的函數(shù)值);
第二步:描點(diǎn)(在直角坐標(biāo)系中�����,以自變量的值為橫坐標(biāo)�����,相應(yīng)的函數(shù)值為縱坐標(biāo)�����,描出表格中數(shù)值對(duì)應(yīng)的各點(diǎn));
第三步:連線(按照橫坐標(biāo)由小到大的順序把所描出的各點(diǎn)用平滑曲線連接起來(lái))�。
8、函數(shù)的表示方法
列表法:一目了然�,使用起來(lái)方便,但列出的對(duì)應(yīng)值是有限的�����,不易看出自變量與函數(shù)之間的對(duì)應(yīng)規(guī)律�。
解析式法:簡(jiǎn)單明了���,能夠準(zhǔn)確地反映整個(gè)變化過(guò)程中自變量與函數(shù)之間的相依關(guān)系���,但有些實(shí)際問(wèn)題中的函數(shù)關(guān)系���,不能用解析式表示。
圖象法:形象直觀�,但只能近似地表達(dá)兩個(gè)變量之間的函數(shù)關(guān)系。
(二)一次函數(shù)Update
1�、一次函數(shù)的定義
一般地,形如
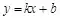
(k�,b是常數(shù),且k≠0)的函數(shù)�����,叫做一次函數(shù)���,其中x是自變量�。當(dāng)b=0時(shí)���,一次函數(shù)y=kx�,又叫做正比例函數(shù)�����。
⑴一次函數(shù)的解析式的形式是
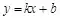
,要判斷一個(gè)函數(shù)是否是一次函數(shù)�,就是判斷是否能化成以上形式.
⑵當(dāng)b=0,k≠0時(shí)�����,y=kx仍是一次函數(shù).
⑶當(dāng)k=0�,b≠0時(shí),它不是一次函數(shù).
⑷正比例函數(shù)是一次函數(shù)的特例�,一次函數(shù)包括正比例函數(shù).
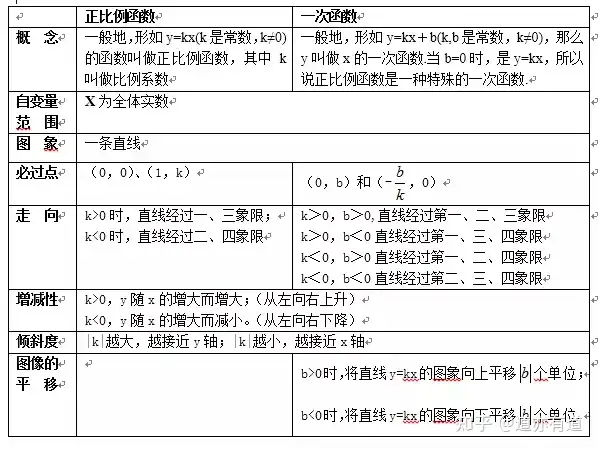
2、正比例函數(shù)及性質(zhì)
一般地�,形如y=kx(k是常數(shù),k≠0)的函數(shù)叫做正比例函數(shù)�����,其中k叫做比例系數(shù).
注:
正比例函數(shù)一般形式 y=kx (k不為零)
① k不為零 ② x指數(shù)為1 ③ b取零
當(dāng)k>0時(shí)�,直線y=kx經(jīng)過(guò)一、三象限�����,從左向右上升���,即隨x的增大y也增大;
當(dāng)k<0時(shí)�,直線y=kx經(jīng)過(guò)二�����、四象限�,從左向右下降,即隨x增大y反而減小.
(1) 解析式:y=kx(k是常數(shù)�����,k≠0)
(2) 必過(guò)點(diǎn):(0�����,0)���、(1�����,k)
(3) 走向:k>0時(shí)�����,圖像經(jīng)過(guò)一���、三象限;k<0時(shí)�,圖像經(jīng)過(guò)
二�、四象限
(4) 增減性:k>0,y隨x的增大而增大;k<0���,y隨x增大而減小
(5) 傾斜度:|k|越大���,越接近y軸;|k|越小,越接近x軸
3�、一次函數(shù)及性質(zhì)
一般地,形如y=kx+b(k,b是常數(shù)�����,k≠0)�,那么y叫做x的一次函數(shù).當(dāng)b=0時(shí),y=kx+b即y=kx���,所以說(shuō)正比例函數(shù)是一種特殊的一次函數(shù).
注:一次函數(shù)一般形式 y=kx+b (k不為零)
① k不為零
②x指數(shù)為1
③ b取任意實(shí)數(shù)
一次函數(shù)y=kx+b的圖象是經(jīng)過(guò)(0�����,b)和(-b/k���,0)兩點(diǎn)的一條直線�,我們稱它為直線y=kx+b,它可以看作由直線y=kx平移|b|個(gè)單位長(zhǎng)度得到.(當(dāng)b>0時(shí)���,向上平移;當(dāng)b<0時(shí),向下平移)
(1)解析式:y=kx+b(k���、b是常數(shù)�����,k≠0)
(2)必過(guò)點(diǎn):(0�����,b)和(-b/k���,0)
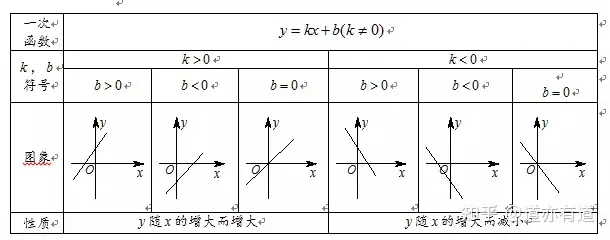
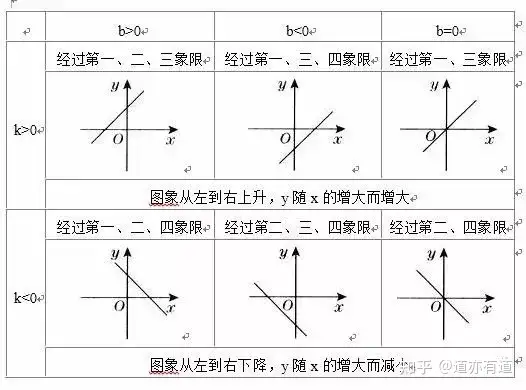
(3)走向:
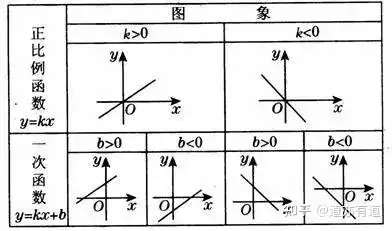
k>0,圖象經(jīng)過(guò)第一�����、三象限;k<0,圖象經(jīng)過(guò)第二�、四象限
b>0,圖象經(jīng)過(guò)第一�����、二象限;b<0�����,圖象經(jīng)過(guò)第三�、四象限
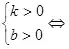
直線經(jīng)過(guò)第一、二�����、三象限
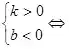
直線經(jīng)過(guò)第一�����、三�����、四象限
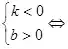
直線經(jīng)過(guò)第一�、二���、四象限
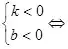
直線經(jīng)過(guò)第二、三�、四象限
(4)增減性: k>0,y隨x的增大而增大;k<0�����,y隨x增大而減小.
(5)傾斜度:|k|越大���,圖象越接近于y軸;|k|越小,圖象越接近于x軸.
(6)圖像的平移:
當(dāng)b>0時(shí)�,將直線y=kx的圖象向上平移b個(gè)單位;
當(dāng)b<0時(shí),將直線y=kx的圖象向下平移b個(gè)單位.
4�����、一次函數(shù)y=kx+b的圖象的畫法.
根據(jù)幾何知識(shí):經(jīng)過(guò)兩點(diǎn)能畫出一條直線�����,并且只能畫出一條直線���,即兩點(diǎn)確定一條直線�,所以畫一次函數(shù)的圖象時(shí),只要先描出兩點(diǎn)�����,再連成直線即可.一般情況下:是先選取它與兩坐標(biāo)軸的交點(diǎn):(0�,b),(-b/k�����,0) .即橫坐標(biāo)或縱坐標(biāo)為0的點(diǎn).
5�����、正比例函數(shù)與一次函數(shù)之間的關(guān)系:一次函數(shù)y=kx+b的圖象是一條直線���,它可以看作是由直線y=kx平移|b|個(gè)單位長(zhǎng)度而得到(當(dāng)b>0時(shí)�,向上平移;當(dāng)b<0時(shí)�,向下平移)
6、正比例函數(shù)和一次函數(shù)及性質(zhì)
6���、直線
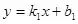
(
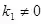
)與
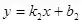
(
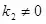
)的位置關(guān)系
(1)兩直線平行
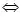
且
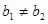
(2)兩直線相交
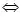
(3)兩直線重合
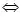
且
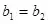
(4)兩直線垂直
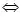
7�����、用待定系數(shù)法確定函數(shù)解析式的一般步驟:
(1)根據(jù)已知條件寫出含有待定系數(shù)的函數(shù)關(guān)系式;
(2)將x�、y的幾對(duì)值或圖象上的幾個(gè)點(diǎn)的坐標(biāo)代入上述函數(shù)關(guān)系式中得到以待定系數(shù)為未知數(shù)的方程;
(3)解方程得出未知系數(shù)的值;
(4)將求出的待定系數(shù)代回所求的函數(shù)關(guān)系式中得出所求函數(shù)的解析式.
歡迎使用手機(jī)、平板等移動(dòng)設(shè)備訪問(wèn)中考網(wǎng)�,2023中考一路陪伴同行!>>點(diǎn)擊查看













