ĪĪĪĪ║▄ČÓ═¼īW─├üĒę╗Ą└Ņ}Š═ķ_╩╝Å─ęčų¬═∙║¾═Ų�����Ż¼═ŲĄĮ╦└║·═¼ĢrŠ═ĘĄ╗žüĒį┘šę┴Ēę╗Śl┬Ę��Ż¼ČÓöĄŪķørŽ┬┴Ēę╗Śl┬Ęę▓╩Ūæęč┬Ū═▒┌�����Ż¼╚╗║¾ĘŁüĒĖ▓╚źĄ─Žļæ¬įōį§├┤ū÷�����ĪŻī¦ų┬▀@ĘNŪķørĄ─įŁę“Š═╩Ū���Ż¼═¼īWéāīÅŅ}▓╗ūą╝Ü�����ĪŻ
ĪĪĪĪ┐┤ę╗Ą└Ņ}���Ż¼ę¬Ž±┐┤ę╗éĆ╚╦ę╗śėŻ¼╚╦╝ęäé┘I┴╦ę╗╝■ą┬ę┬Ę■��Ż¼─ŃęŖ├µŠ═┐õ╚╦╝ęĄ─┼fčØūėČÓ├┤ČÓ├┤Ų»┴┴��Ż¼▀@╩Ū┐ŽČ©▓╗ąąĄ─�����Ī����Ż┐┤Ņ}ĢrŻ¼ę¬Å─ęčų¬Śl╝■│÷░l(f©Ī)�����Ż¼┐┤ę╗Ž┬ęčų¬Śl╝■ųąĄ──Ūą®Śl╝■╩ŪŅ}č█Ż¼╩Ū×ķ╬ęéā╠ß╣®╦╝┬ĘĄ─ĻPµI��ĪŻ╩┬īŹ╔Ž�����Ż¼▀@ĘN─▄┴”ę╗╩ŪĮ©┴óį┌ę╗Č©Ą─ū÷Ņ}┴┐Ą─╗∙ĄA╔Ž�Ż¼Ė³ųžę¬Ą─╩Ūī”ė┌╗∙ĄAų¬ūRĄ─└ĒĮŌ║═░č╬šŻ¼▀@ę▓╩Ū╬ęę╗ž×ÅŖš{Ą─��Ī�����Ż╗∙ĄAį·īŹ��Ż¼─▄ē“ņ`╗Ņ▀\ė├�����Ż¼į┘╝ė╔Ž▀m«ö┐éĮY�����Ż¼ļS▒Ń─├üĒę╗Ą└Ņ}���Ż¼ūx═ĻŅ}����Ż¼─▄ė├ĄĮĄ─ĘĮĘ©ę▓Š═│÷üĒ┴╦����ĪŻ
ĪĪĪĪŽ┬├µ┼eéĆ└²ūėšf├„╚ń║╬Å─Ņ}─┐ųąĘų╬÷│÷üĒū÷Ņ}Ą─ĘĮĘ©ĪŻ═¼īWéāį┌ū÷Ņ}«öųąĮø│ŻĢ■ė÷ĄĮ▒╚▌^ā╔ŚlŠĆČ╬ķLČ╚Ą─å¢Ņ}��ĪŻ▀@ŅÉå¢Ņ}╬ęį┌Į╠īW▀^│╠ųąŽ▓ÜgūīīW╔·éā▓┬┤░Ė�����ĪŻę“×ķ▀@ĘN▓┬£y╩ŪĮ©┴óį┌šJšµūxŅ}Ą─╗∙ĄA╔ŽĄ─��ĪŻ“šł▒╚▌^ŠĆČ╬AB║═CDĄ─öĄ┴┐ĻPŽĄ”║═“šł▒╚▌^ŠĆČ╬AB║═CDĄ─┤¾ąĪ”▀@ā╔éĆå¢Ņ}┐┤╦Ųę╗śė�����Ż¼Ą½╩Ūę╗░ŃĄ─墓öĄ┴┐ĻPŽĄ”Ą├ĄĮĄ─═∙═∙╩ŪĄ╚╩Į�����Ż¼╝┤AB=CD╗“AB=1/2CDĄ╚Ą╚Ż¼å¢“┤¾ąĪĻPŽĄ”Ą├ĄĮĄ─ėą┐╔─▄╩ŪĄ╚╩Įę▓ėą┐╔─▄╩Ū▓╗Ą╚╩Į�����Ż¼╚¶╩ŪĄ╚╩Į�Ż¼ČÓöĄŪķør╩Ūęį1Ż║1ŽÓĄ╚Ą─Ūķør│÷¼F╝┤AB=CDŻ¼«ö╚╗�����Ż¼▀Ćę¬┼õ║ŽŠ▀¾wĄ─Ņ}─┐łDą╬�ĪŻę“┤╦╬ęĢ■ĖµįVīW╔·Ż¼å¢Ņ}╠ßå¢Ą─ą╬╩Į�����Ż¼═∙═∙ę▓Ģ■▓╗ĮøęŌķg═Ė┬Č│÷ę╗ą®┤░Ė����ĪŻ
ĪĪĪĪ╔Ž├µų╗╩Ūę╗ą®ąĪ╝╝Ū╔Ż¼ĮėŽ┬üĒ╬ęéāūx═ĻŅ}ķ_╩╝šę╦╝┬Ę�����ĪŻ▒╚▌^ŠĆČ╬Ą─┤¾ąĪĻPŽĄĄ─å¢Ņ}�Ż¼═©│Żėą╦─ĘNŪķør
ĪĪĪĪŻ©1Ż®aĪĘb��Ż╗
ĪĪĪ�����ĪŻ©2Ż®a+bĪĘc��Ż╗
ĪĪĪ��ĪŻ©3Ż®a+bĪĘc+d��Ż╗
ĪĪĪ��ĪŻ©4Ż®a+b+cĪĘd���ĪŻŻ©“ĪČ”Ą─Ūķør═¼└ĒŻ®
ĪĪĪĪ╦╝┬ĘÅ─║╬Č°üĒ�����Ż¼Å─╗∙ĄAų¬ūRČ°üĒ���ĪŻ─Ū├┤╩ūŽ╚╬ęéāę¬╗žŽļį┌│§ųąļAČ╬Č╝īW▀^╩▓├┤ĻPė┌ŠĆČ╬ķLČ╚Ą─Č©└ĒŻ¼├┐ŚlČ©└Ē║¾├µėųėą╩▓├┤ų¬ūR³c─žĪŻ╬ęéāę╗Ų┐┤ę╗Ž┬Ż║
ĪĪĪĪ1�����Īó┤╣ŠĆČ╬ūŅČ╠
ĪĪĪĪ→ų▒ĮŪ╚²ĮŪą╬ųąą▒▀ģ┤¾ė┌ų▒ĮŪ▀ģ
ĪĪĪĪ2����Īóā╔³cų«ķgŠĆČ╬ūŅČ╠
ĪĪĪĪ→╚²ĮŪą╬ā╔▀ģų«║═┤¾ė┌Ą┌╚²▀ģ
ĪĪĪĪ→╚²ĮŪą╬ųąā╔▀ģų«▓ŅąĪė┌Ą┌╚²▀ģ
ĪĪĪĪ→░╦ūųą╬┼c’wńS─Żą═
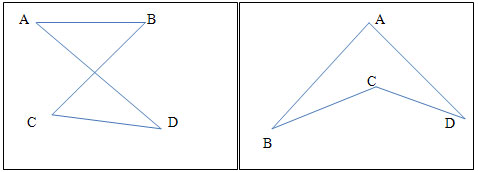
ĪĪĪĪį┌░╦ūųą╬ųąŻ¼AB+CDĪČAD+CB���Ż¼į┌’wńS─Żą═ųąAB+ADĪĘBC+CD��Ż¼ūóęŌ��Ż¼▀@ā╔éĆ─Żą═Ą─ĮYšō▓╗─▄ē“ų▒Įė╩╣ė├��Ż¼Ą½╩Ū┐╔ęį×ķ╬ęéāĄ─Ū¾ūC╠ß╣®ę╗éĆ┴╝║├Ą─╦╝┬Ę���ĪŻ
ĪĪĪĪų¬ūR³c╗žæø═Ļ┴╦Ż¼╬ęéāĮėŽ┬üĒ┐┤å¢Ņ}����Ż¼╚ń╣¹╩ŪŻ©1Ż®ųąĄ─ŪķørŻ¼╬ęéā╩ūŽ╚ŽļĄĮĄ─╩Ū1Ą─ĘĮĘ©���Ż¼Š═╩Ū▀\ė├ų▒ĮŪ╚²ĮŪą╬ą▒▀ģ┤¾ė┌ų▒ĮŪ▀ģ����Ż¼╚ń╣¹░l(f©Ī)¼F╦∙ĮoĄ─ā╔ŚlŠĆČ╬▓╗į┌═¼ę╗éĆų▒ĮŪ╚²ĮŪą╬ųą��Ż¼─Ū├┤Š═ꬎļĄĮĄ─═©▀^ŲĮęŲ╗“śŗįņŲĮąą╦─▀ģą╬����Ż¼īóā╔ŚlŠĆČ╬Ę┼ĄĮ═¼ę╗éĆų▒ĮŪ╚²ĮŪą╬ųąüĒĮŌøQå¢Ņ}ĪŻ╚ń╣¹1ųąĄ─ĘĮĘ©▒╚▌^┬ķ¤®��Ż¼▀@Ģr╬ęéāę¬─▄ŽļĄĮ░čå¢Ņ}▐D╗»│╔Ż©2Ż®Ą─ŅÉą═�����Ż¼▀\ė├2Ą─ĘĮĘ©üĒĮŌøQ�ĪŻ▀@ĘNĘĮĘ©Š═╩Ū╬ęéā│ŻšfĄ─“ĮžķLčaČ╠”Ż¼░č▌^ķLĄ─ę╗ŚlŠĆČ╬▓│╔ā╔Śl��Ż¼ūī▀@ā╔ŚlŠĆČ╬║═╩ŻŽ┬Ą──Ūę╗ŚlŠĆČ╬śŗ│╔╚²ĮŪą╬�Ż¼▀\ė├“╚²ĮŪą╬ā╔▀ģų«║═┤¾ė┌Ą┌╚²▀ģ“üĒĮŌøQŻ¼═¼śė��Ż¼╚ń╣¹▀@ÄūŚlŠĆČ╬▓╗į┌═¼ę╗éĆ╚²ĮŪą╬ā╚��Ż¼ę¬Žļ▐kĘ©═©▀^ŲĮęŲ╗“śŗįņŲĮąą╦─▀ģą╬īó╦¹éāĘ┼į┌ę╗ŲĪŻ▀@└’ąĶę¬ūóęŌ��Ż¼Įø│Żė├ĄĮĄ─▀Ćėąę╗éĆĘĮĘ©����Ż¼Š═╩ŪĮž╚Ī▌^ķLŠĆČ╬Ż¼═©▀^╚½Ą╚╗“Ųõ╦¹ĘĮĘ©ūC├„Ųõųą─│ę╗Č╬Ą╚ė┌įŁŽ╚─ŪŚl▌^Č╠Ą─ŠĆČ╬�Ż¼▀@└’ė├Ą─īŹļH╔ŽŠ═╩ŪąĪīWĄ─▒╚▌^┤¾ąĪĄ─ĘĮĘ©ĪŻ
ĪĪĪĪ╚ń╣¹╩ŪŻ©2Ż®Ą─Ūķørę╗░ŃĄ─����Ż¼ų▒Įė▀\ė├2Ą─ĘĮĘ©üĒĮŌøQŻ¼╝┤īó╚²ŚlŠĆČ╬Ę┼ĄĮ═¼ę╗éĆ╚²ĮŪą╬ųą╚ź��ĪŻį┌─│ą®ŪķørŽ┬ę▓┐╔ęį═©▀^śŗįņ╚½Ą╚╚²ĮŪą╬╗“š▀ŲĮęŲ���Ż¼īóā╔ŚlŠĆČ╬║Ž▓ó╗žÜwĄĮ1Ą─ĘĮĘ©ųą╚ź�ĪŻ
ĪĪĪĪ╚ń╣¹╩ŪŻ©3Ż®Ą─Ūķør��Ż¼┐╔ęį═©▀^║Ž▓óŠĆČ╬����Ż¼▐D╗»×ķŻ©2Ż®╗“Ż©1Ż®Ą─å¢Ņ}▀MąąĮŌ┤Ż¼ę▓┐╔ęįśŗįņ’wńS─Żą═┼c░╦ūųą╬����Ż¼═©▀^ęčų¬─Żą═╦─ŚlŠĆČ╬ų«ķgĄ─ĻPŽĄ▀Mąą▌oų·ŠĆĄ─╠Ē╝ė�����Ż¼Å─Č°Ū¾ūC�ĪŻ
ĪĪĪĪ╚ń╣¹╩ŪŻ©4Ż®Ą─Ūķør�����Ż¼ę╗░ŃĄ─═©▀^║Ž▓óŠĆČ╬▐D╗»×ķŻ©2Ż®Ż©1Ż®Ą─å¢Ņ}▀MąąĮŌ┤�����ĪŻ
ĪĪĪĪå¢Ņ}╚½├µĄ─Ęų╬÷═Ļ┴╦�����Ż¼▀@ą®Č╝āHāH╩ŪÅ─å¢Ņ}╚ļ╩ųüĒĄ├│÷Ą─ĘĮĘ©�Ż¼╚ń╣¹į┘┼õ║ŽŚl╝■�����Ż¼─▄ē“▀Mę╗▓Į├„┤_ĘĮĘ©��ĪŻę╗░ŃĄ─Ż¼▀@ĘNå¢Ņ}▌oų·ŠĆĄ─«ŗĘ©ėą║▄ČÓ����Ż¼Ū¾ūCĄ─ĘĮĘ©ę▓Ģ■ČÓĘNČÓśėŻ¼ę“┤╦į┌ŲĮ│Żū÷Ņ}Ą─Ģr║“▓╗Ę┼├┐ĘNĘĮĘ©Č╝ćLįćę╗Ž┬�����Ż¼×ķūį╝║ČÓ│┴ĄĒą®ĮŌŅ}╦╝┬Ę�����ĪŻ
ūŅ║¾��Ż¼ūŻįĖ┤¾╝ęį┘ūŅ║¾Ą─Äū╩«╠ņ└’����Ż¼į┘╝ė░╔ä┼Ż¼╚ĪĄ├Ė³║├Ą─│╔┐ā�ŻĪ
ĪĪĪĪ ÜgėŁ╩╣ė├╩ųÖCĪóŲĮ░ÕĄ╚ęŲäėįOéõįLå¢ųą┐╝ŠW��Ż¼2024ųą┐╝ę╗┬Ę┼Ń░ķ═¼ąą��ŻĪ>>³cō¶▓ķ┐┤










